Financial markets are shaped by complex volatility patterns that standard models often fail to reproduce. Rough volatility models capture these fine-scale effects, but their accuracy depends entirely on how the underlying fractional processes are simulated.
Our new L2-Exact Riemann–Liouville (RL) scheme removes the long-standing simulation bias seen in conventional methods like the BLP Hybrid approach. The result is variance-exact rough volatility simulation that remains fully causal and computationally efficient, crucial for reinforcement-learning and AI systems that train on sequential data.
Compared to the industry-standard Hybrid method, which systematically underestimates variance at small scales, the RL L2-Exact method matches theoretical behavior with high precision while keeping compatibility with stochastic differential equation solvers.
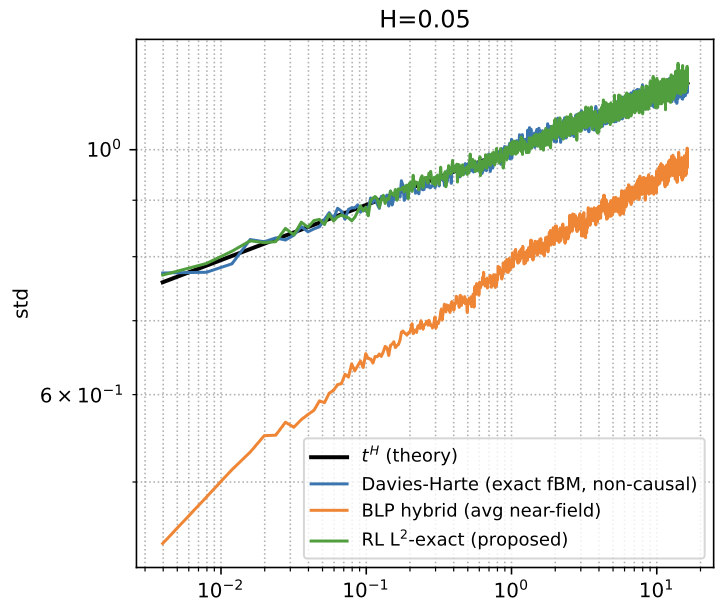
Standard deviation vs. time for H=0.05. The L2-Exact RL (green) matches theoretical scaling, removing bias found in the Hybrid method (orange).
For businesses developing financial AI, this means:
- More realistic synthetic data for model training
- Faster convergence of pricing and risk models
- Reliable reinforcement-learning environments that mirror real-world dynamics
The method is simple to implement, variance-consistent at every scale.
You can find all technical details, proofs, and benchmarks in the paper Variance-Exact Simulation of Rough Volatility: A Comparison of Hybrid, Davies-Harte, and L2-Exact Riemann-Liouville Schemes
